In this section, we briefly review two methods to compute the reflection point on a quadric surface reflector when reflecting a light traveling from a known source to a known destination - our Quadric Intersection Method (QI Method) and the Mitsubishi Method (since it has been developed in the Mitsubishi Labs).

In our QI Method an additional constraint on the reflection point is imposed, allowing a much faster way to search for the actual reflection point. This constraint states that the reflection point belongs not only to the reflector surface but also belongs to an analytical quadric whose expression depends exclusively on the geometry of the projection (center of projection and 3D point to be projected). Since the searched reflection point belongs to these two quadrics, it shall be searched in their intersection. The parametric curve given by the intersection algorithm is a function of only one parameter, say λ.
Read more...

The Mitsubishi Method presented by Agarwal, Taguchi and Ramalingam derives explicit expressions for the coefficients of an 8th degree polynomial whose solutions contain the reflection point R. It is based on two intermediate equations whose intersection gives a parameterization of the solution in a polynomial.
Read more...

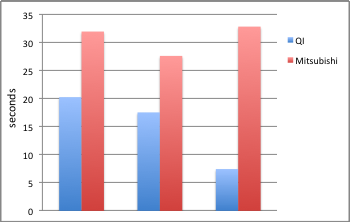
We designed a comprehensive set of experiments to fully test both methods in several conditions and measured the execution time, excluding overhead phases so that the performance evaluated are for the exact computation of the reflection point. All tests were made using 100,000 points. As shown in the graphic above, that shows the total execution time for the computation of the reflection point using a spherical mirror, our method is between 2 and 5 times faster than the Mitsubishi Method, computing a reflection point in average 10 micro-seconds.

The position of the 3D point was randomly generated at the beginning of each iteration where we compute the execution time for both methods (hence with the same point). The implementation code was all written in C++ language and the tests were performed in a desktop equipped with an 3.4 GHz Intel Core i7.

We are studying the possibility to speed-up the QI Method using the results of the previous point in the following 3D point projection. This spatial locality phenomenon can be explained by the fact that when the best reflection point is searched in the proximity of the best solution for the previous point, the probability of finding the solution very closely is high. Since the Mitsubishi Method is based on the solution of an 8th degree polynomial, there is no spatial locality effect that enhances its performance. With Mitsubishi Method all polynomial coefficients must be recomputed for each 3D point, which is computationally heavy. Also, the expressions of their polynomial coefficients include circa 55.000 expensive math computations.

In what concerns to real-time applications using the QI Method, it computes a reflection point in an average of 0.3 micro-seconds, making it perfectly suitable for real-time applications, mainly if one attend the fact that further accelerations are being studied and a GPU implementation is also intended for it.